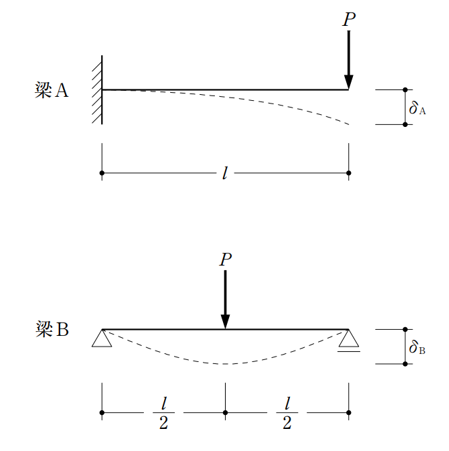
〔Ｎｏ． 1〕 図のような集中荷重Pを受ける梁Ａ及びＢの荷重点に生じるたわみδAとδBとの比として、正しいものは、次のうちどれか。ただし、梁Ａ及びＢは同一断面で、全長にわたって等質等断面の弾性部材とし、自重は無視する。
|
|
| δA : δB |
| 4 ： 1 |
| 8 ： 1 |
| 16 ： 1 |
| 32 ： 1 |
|
ゆこ
この問題は、公式を覚えているか覚えていないかで得点できるかどうかが決まります。構造力学の公式はたくさんあって覚えるのが大変ですが、できるだけ覚えておきたいですね。
解答と解説 詳細を見る
梁A
先端に集中荷重が作用している片持ちばりのたわみδを求める公式は、
$$\frac {Pl^3}{3EI}$$
梁B
中央に集中荷重が作用している単純ばりのたわみδを求める公式は、
$$\frac {Pl^3}{48EI}$$
この２つを比較すると、16：1 となります。
公式を覚えていると、簡単に答えを導き出すことができますね。
≪正解3≫
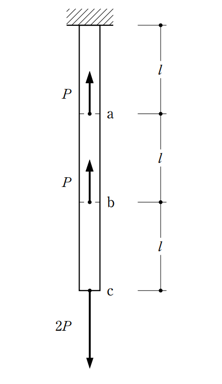
〔Ｎｏ． 2〕 図のような断面積が一定で長さが3lの部材において、ａ、ｂ及びｃの位置における断面の図心にそれぞれ軸方向力P、P及び 2Pが矢印の向きに作用するとき、「ａ－ｂ間の軸力」と「ｃの軸方向変位」との組合せとして、正しいものは、次のうちどれか。ただし、部材は全長にわたって等質等断面の弾性部材とし、自重は無視する。また、部材の断面積をA、ヤング係数をEとする。
|
|
| a－b間の軸力 |
cの軸方向変位 |
| P |
$$\frac {2l}{AE}P$$ |
| P |
$$\frac {3l}{AE}P$$ |
| 2P |
$$\frac {2l}{AE}P$$ |
| 2P |
$$\frac {3l}{AE}P$$ |
|
ゆこ
軸力と変位量を求める問題です。どれくらいの力で押されてどれだけ縮んだか、もしくはどれくらいの力で引っ張られてどれだけ伸びたか。これを考えます。
解答と解説 詳細を見る
まず軸力から求めてみます。
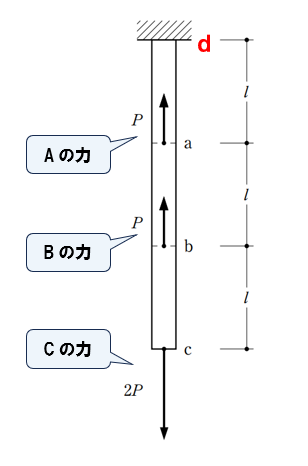
部材が取り付いている部分をｄ点とし、３つの力をそれぞれ、Aの力、Bの力、Cの力とします。
d－a間の軸力
Aの力とBの力に押されCの力に引っ張られています。
上向きにPが２つ、下向きに2Pで、軸力は±0となります。
a－ｂ間の軸力
Bの力に押されCの力に引っ張られています。
上向きにP、下向きに2Pで、軸力は下向きにPとなります。 これが答え
Aの力はd－a間を押すだけであって、a－ｂ間には作用しません。
ｂ－ｃ間の軸力
Cの力に引っ張られています。
下向きに2Pで、軸力は下向きに2Pとなります。
AとBの力はｂ－ｃ間には作用しません。
次に変位量を考えてみましょう。
変位量（Δl）の求め方ですが、変位量には次の４つの要素が関係してきます。
- 部材にかかる力（N ）・・・大きいほど変位量は大 ⇒ 比例
- 部材の長さ（ l ）・・・長いほど変位量は大 ⇒ 比例
- 部材のヤング係数（E ）・・・大きいほど変位量は小 ⇒ 反比例
- 部材の断面積（A ）・・・大きいほど変位量は小 ⇒ 反比例
ヤング係数とは、部材の変形のしにくさ。大きいほど変形しにくい。
ということで、変位量を求める計算式は次のようになります。
$$Δl=\frac {Nl}{AE}$$
ゆこ
比例するものが分子で、反比例するものが分母ですね。
問題ではｃにおける変位量を求めていますので、３つの区間全ての変位量を求めて合計すればOKです。
それぞれ公式に当てはめてみます。
d－a間の変位量
軸力が0なので、変位量はありません。
a－ｂ間の変位量
公式のNのところにPを代入します。
$$\frac {Pl}{AE}$$
ｂ－ｃ間の変位量
公式のNのところに2Pを代入します。
$$\frac {2Pl}{AE}$$
２つを足すと
$$\frac {Pl}{AE}＋\frac {2Pl}{AE}＝\frac {3Pl}{AE}$$
ということで正解は、軸力がP 変位量は、
$$\frac {3l}{AE}P$$ ということになりました。
≪正解2≫
【一級建築士試験 学科クラブ】わからない時はいつでも質問可能／15年分の過去問題取り組み
一級の学科試験、独学か、それとも通学か
一級建築士の学科試験
そのハードルは、決して低くはない。
おそらく、多くの受験生がそう...
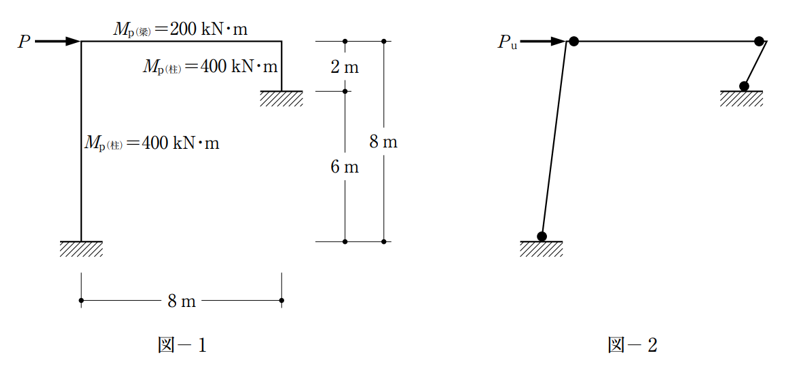
〔Ｎｏ． 3〕 図－ １ のような水平荷重Pを受けるラーメンにおいて、Pを増大させたとき、そのラーメンは、図－ ２ のような崩壊機構を示した。ラーメンの崩壊荷重Puの値として、正しいものは、次のうちどれか。ただし、柱、梁の全塑性モーメントの値は、それぞれ 400 kN･m、200 kN･mとする。
- 225 kN
- 300 kN
- 375 kN
- 500 kN
ゆこ
この問題は、仮想仕事の原理を利用して求めます。慣れるまでは難しく感じると思いますが、慣れてしまえばそれほど難しくありません。出題頻度は高いと言えますので、できるだけ攻略しておきたい問題です。
解答と解説 詳細を見る
仮想仕事の原理とは
外力のなす仕事量と構造内部に働く内力（軸力，曲げモーメント， せん断力）のなした仕事量が釣り合う（等しくなる）という原理です。
この問題を解く場合、まずはじめに塑性ヒンジが生じた時の崩壊メカニズムの図を描きます。
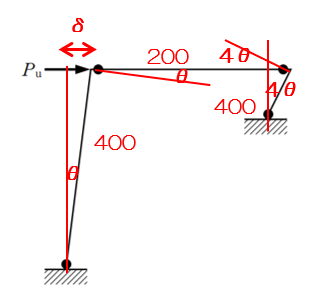
左側の柱の回転角をθとした場合、右側の柱は長さが1/4なので、回転角は４倍の４θとなります。
外力による仕事は、荷重（Pu）×変位量（δ）で求めます。
変位量（δ）は、部材の長さ×回転角（θ）
よって、外力のなす仕事は、Pu×δ ＝ Pu×8×θ
内力による仕事は、全ての塑性ヒンジの全塑性モーメント×回転角の合計となります。
柱と梁の接合部における塑性ヒンジは、全塑性モーメントの小さい方の部材の端部に生じます。よって、この問題の場合は梁の端部に生じます。
内力による仕事は、400×θ＋200×θ＋200×4θ＋400×4θ ＝ 3000θ
Pu×8×θ と 3000θ が等しくなりますので、Pu×8×θ ＝ 3000θ
Pu= 375ｋN となります。
≪正解3≫
〔別解〕モーメント図を用いて解く方法
２本の柱に生じているせん断力（柱を横にずらそうとする力）の合計は、水平荷重Puと等しくなります。これを利用して解く方法です。
モーメント図を描くと下図のようになります。
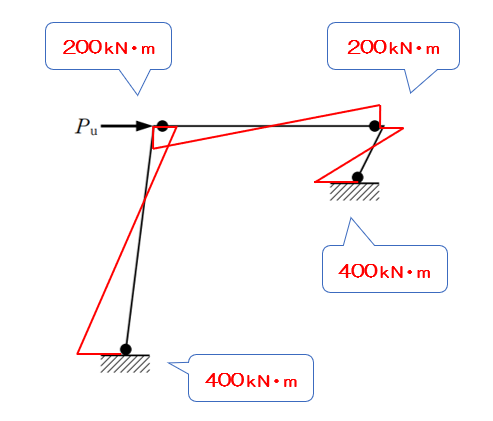
せん断力は、次の式で求めることができます。
$$\frac {両端のモーメントの合計}{部材の長さ}$$
左の柱のせん断力は、
$$\frac {200＋400}{8}＝75$$
右の柱のせん断力は、
$$\frac {200＋400}{2}＝300$$
左の柱と右の柱のせん断力を合わせると375ｋN。これが崩壊荷重Puとなります。
〔Ｎｏ． 4〕 図は、2層のラーメンにおいて、 2 階に水平荷重P1、Ｒ階に水平荷重P2 が作用したときの柱の曲げモーメントを示したものである。次の記述のうち、誤っているものはどれか。ただし、全ての部材の自重は無視する。
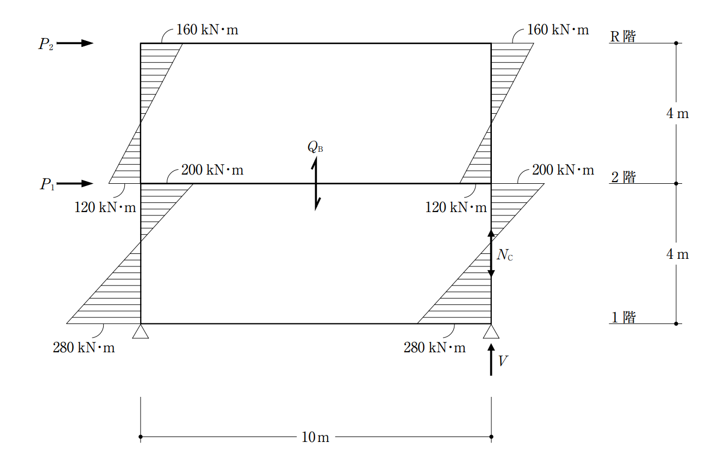
- 2 階に作用する水平荷重P1 は、100 kNである。
- 2 階の梁のせん断力QBは、64 kNである。
- 1 階右側の柱の軸方向圧縮力NCは、128 kNである。
- 右側の支点の鉛直反力Vは、152 kNである。
ゆこ
この問題も過去によく出題されている問題です。少しややこしそうですが、コツをつかむとできるようになると思います。何回か解いてみてください。慣れるとそれほど難しくは感じなくなると思います。
解答と解説 詳細を見る
➊水平荷重は、柱に生じているせん断力から導き出すことができます。
せん断力は、次の式により求めます。
$$せん断力＝\frac {両端のモーメントの合計}{部材の長さ}$$
１階の柱に生じているせん断力は、P2とP1の両方によるものです。２階の柱に生じているせん断力はP2だけです。なので、手順としては
- ２階の柱に生じているせん断力からをP2求める。
- １階の柱に生じているせん断力から（P1＋P2）を求める。
- （P1＋P2）からP2を引く
ということで、求めてみましょう。
$$２階柱のせん断力＝\frac {160＋120}{4}＝70ｋN$$
柱は２本ありますので、２倍の140ｋN。これがP2の力です。
１階の柱のせん断力は
$$１階柱のせん断力＝\frac {200＋280}{4}＝120ｋN$$
同じく２倍して240ｋN。これが（P1＋P2）合わせた力です。
ここから、P2を引けば、P1が求まります。
（P1＋P2）－P2＝ 240ｋN－140ｋN＝100ｋN
ということで、選択肢➊は正しい。
➋2階の梁のせん断力QBは、両端のモーメントの合計をスパン（距離）で割って求めます。
$$\frac {（120＋200）×２か所}{10}＝64ｋN$$
ということで、選択肢➋も正しい。
➌柱の軸方向力NCは、R階梁のせん断力と2階梁のせん断力の合計になります。せん断力の求め方は、同じく
$$せん断力＝\frac {両端のモーメントの合計}{部材の長さ}$$
ということで、Ｒ階の梁のせん断力は
$$\frac {160×2か所}{10}＝32ｋN$$
２階の梁のせん断力は
$$\frac {（120＋200）×2か所}{10}＝64ｋN$$
２つを合わせると、32ｋN＋64ｋN＝96ｋN となります。
柱の軸方向力NCは、96ｋNです。
➌が誤りですね。
➍支点の反力Vは、全ての梁のせん断力の合計となります。
１階の梁のせん断力は
$$\frac {280×2か所}{10}＝56ｋN$$
R階梁と２階の梁のせん断力はそれぞれ32ｋNと64ｋNなので、３つを合わせると
32ｋN＋64ｋN＋56ｋN＝152ｋN
支点の反力Vは、152ｋNとなります。➍は正しいです。
≪正解3≫
〔Ｎｏ． 5〕 静定トラスは、一つの部材が降伏すると塑性崩壊する。図のような集中荷重Pを受けるトラスの塑性崩壊荷重として、正しいものは、次のうちどれか。ただし、各部材は、断面積をA、材料の降伏応力度をσyとし、断面二次モーメントは十分に大きく、座屈は考慮しないものとする。また、全ての部材の自重は無視する。
|
|
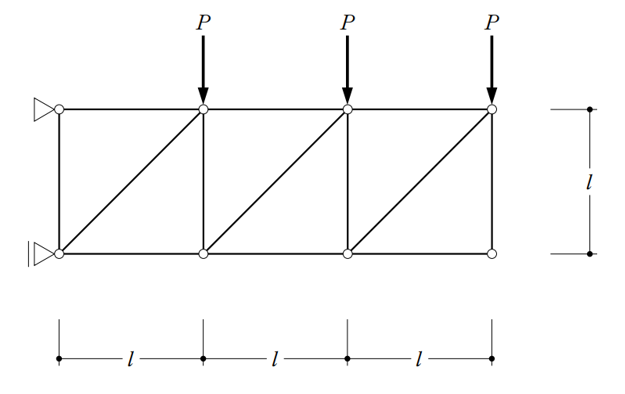
| $$\frac {Aσy}{3}$$ |
| $$\frac {Aσy}{3\sqrt{2}}$$ |
| $$\frac {Aσy}{6}$$ |
| $$\frac {Aσy}{6\sqrt{2}}$$ |
|
ゆこ
この問題は、集中荷重であるPがいくつであれば、トラスが崩壊するか、というものです。
まずは、一番大きく荷重を負担している部材を見つける必要がありますよ。
解答と解説 詳細を見る
降伏応力度σｙとは、降伏する時の力ですが、応力度なので単位面積あたりの力となります。
つまり、降伏する時その部材に生じている実際の力は、σｙ×A（面積）で求めることができます。
この問題の攻略ポイントは４つ
- 最も大きな応力（軸方向力）が生じている部材を見つける。
- 応力を求めるには切断法を用いる。
- その部材に生じている応力とσｙ×Aは等しい。
- 応力＝σｙ×A となるようPの値を求める。
問題の焦点となっている一番応力が生じている部材ですが、何となくピンとローラーで支えられている左側の方の部材であることは予想がつくと思います。なので、下図の赤線部分で切断してみたいと思います。
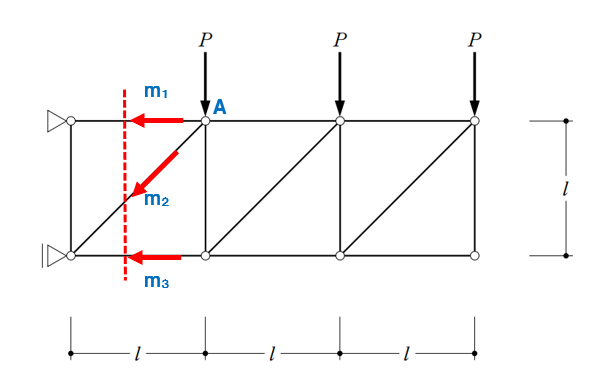
ｍ１の応力を求める
ｍ2とｍ3が交わるローラー部分を基準にし、点線から右側部分の力（3つの外力Pと切断された３つの部材の力）がつり合うことから式を立てます。
計６つの力のモーメントがつり合います。∑M＝０ です。
切断された部材は、切り口に向かう方に力の向きを設定します。（反対でもOKです。）
P×ｌ＋P×2ｌ＋P×3ｌ－ｍ１×ｌ＝ 0 ⇒ ｍ１＝6P
答えが＋になりましたので、想定した向きとなります。
節点から離れる向きなので引張材です。
ｍ3の応力を求める
ｍ1とｍ2が交わるA点を基準にモーメントのつり合いを考えます。
P×ｌ＋P×2ｌ＋ｍ3×ｌ＝0 ⇒ ｍ3＝－3P
答えが－になりましたので、想定した向きとは反対になります。
節点に向かう向きなので圧縮材です。
ｍ2の応力を求める
鉛直方向のつり合い方程式 ΣY＝0 より
$$－3P－\frac {1}{√2}×ｍ2＝0 ⇒ ｍ2＝－3√2P$$
答えが－になりましたので、想定した向きとは反対になります。
節点に向かう向きなので圧縮材です。
一番大きな応力が生じているのは、6Pのｍ１になります。
この6Pがσｙ×Aと等しくなりますので、
$$6P=σy×A ⇒ P=\frac {Aσy}{6}$$
≪正解3≫
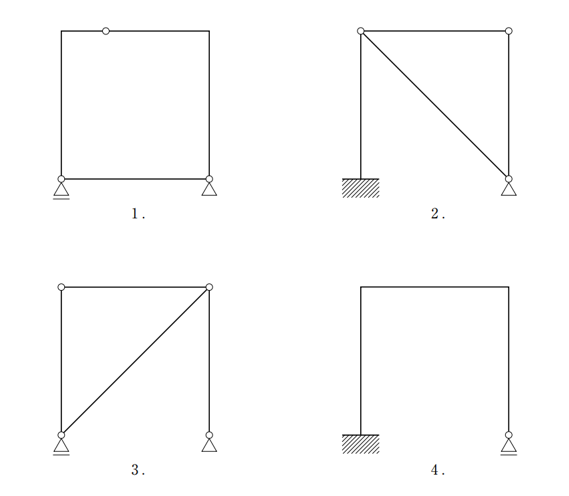
〔Ｎｏ． 6〕 次の架構のうち、静定構造はどれか。
ゆこ
この問題は、解き方さえ知っていれば正解できる問題と言えます。過去にも出てきていますし今後の出題の可能性もあると言えますので、是非できるようになっておいてください。
解答と解説 詳細を見る
静定構造とは、力のつり合い方程式 (ΣX=0、ΣY=0、ΣM=0) により反力や応力を求めることが出来る構造物のこと。反力は３つです。
不静定構造とは、力のつり合い方程式で反力や応力を求めることができない構造物をいいます。反力は４つ以上となります。
静定構造、不静定構造は、次の式によって判別することができます。
ｍ ＝（ｎ＋ｓ＋ｒ）－2ｋ
ｍ＝0 ⇒ 安定、静定構造
ｍ＞0 ⇒ 安定、不静定構造
ｍ＜0 ⇒ 不安定構造
ｎ：反力数
ｓ：部材数
ｒ：剛節接合部材数（1つの部材に対して、剛接合された部材の数の合計）
ｋ：節点数
上の式に代入します。
➊ ｍ＝3＋５＋２－2×５＝0 ⇒ 静定構造
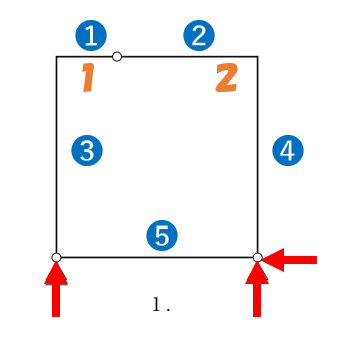
反力 3
部材数 5
剛節接合部材数 2
節点数 5
➋ ｍ＝5＋4＋0－2×4＝1 ⇒ 不静定構造
反力 5
部材数 4
剛節接合部材数 0
節点数 4
➌ ｍ＝3＋4＋0－2×4＝－1 ⇒ 不安定構造
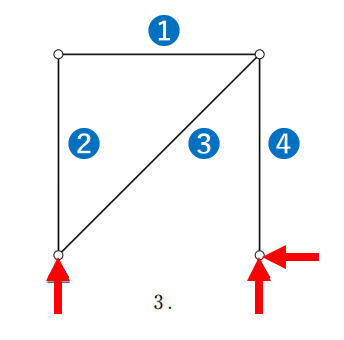
反力 3
部材数 4
剛節接合部材数 0
節点数 4
➍ ｍ＝4＋3＋2－2×4＝1 ⇒ 不静定構造
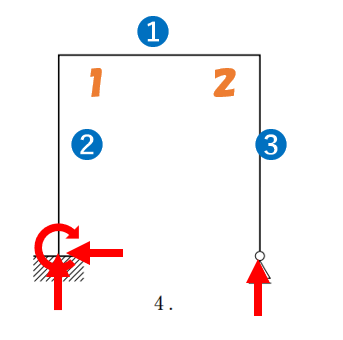
反力 4
部材数 3
剛節接合部材数 2
節点数 4
ということで、正解は１となります。
≪正解1≫
【一級建築士試験 学科クラブ】わからない時はいつでも質問可能／15年分の過去問題取り組み
一級の学科試験、独学か、それとも通学か
一級建築士の学科試験
そのハードルは、決して低くはない。
おそらく、多くの受験生がそう...
