[mathjax]
構造力学
1断面の性質
〔No. 1〕 図のような断面において、図心を通りX軸に平行な図心軸に関する断面二次モーメントの値として、正しいものは、次のうちどれか。
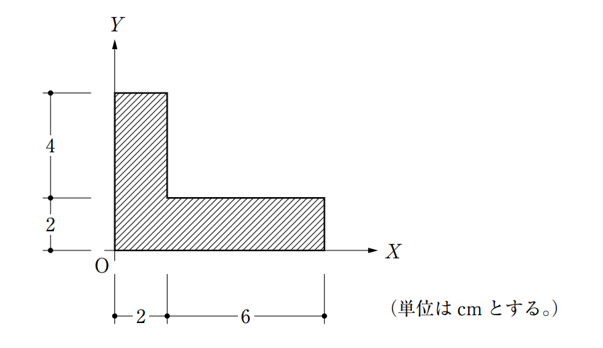
- 40 cm4
- 64 cm4
- 88 cm4
- 112 cm4
- 160 cm4
ゆこ
この問題は、基準となる軸が図心と一致しない場合の断面二次モーメントの公式を覚えていないと解けない問題です。20年ぶりにこの公式が必要になりました。この問題は少し難しい問題と言えそうです。
解答と解説 詳細を見る
この問題のポイント(手順)は2つ
- まず図形全体の図心位置を求める
- その図心に関する断面二次モーメントを求める
1については断面一次モーメントを利用して解きます。これは過去に何度も出題されています。同じように解けばOKです。
その次の断面二次モーメントですが、図形がL型をしていますので、2つの長方形に分けて求め、その2つを合計します。ただし、それぞれ長方形の図心位置(長方形の中心)が、L型図形の図心軸とずれているので注意が必要です。軸と図心が一致しない場合の公式は次のようになります。
$$\frac {bh^{3}}{12}+bhyo^{2}$$
(yo:軸と図心がずれている距離)
軸と図心が一致する場合は、yoが0ということなので、
$$bhyo^{2}$$
も0になります。したがってはじめの部分、 $$\frac {bh^{3}}{12}$$のみで求めることができます。
ゆこ
ここ数年の断面二次モーメントの問題はこの公式で解けていたのですが、ずれている場合の公式も覚えておく必要があると言えそうですね。
全体(L型)図形の図心位置を求める
図心位置は、断面一次モーメントを利用して解きます。L型の図形は2つの長方形に分けて考えてください。左右に分けても上下に分けてもOKです。結果は同じになります。
ここでは、左右に分けた場合の解説をします。
断面一次モーメントの求め方は、面積×距離(軸から図心まで)
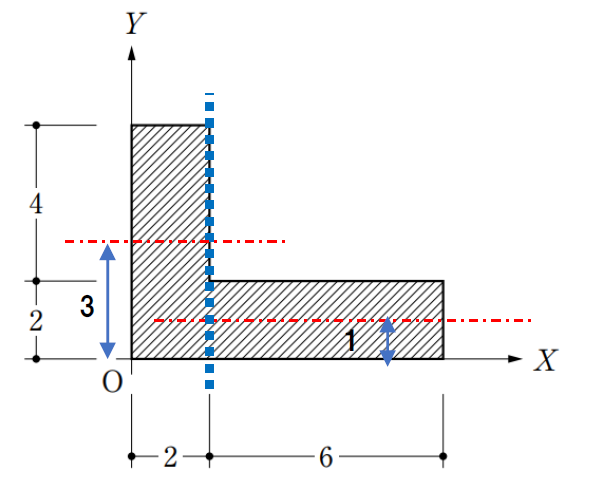
左の長方形 X軸から図心までの距離は3cm
よって断面一次モーメントは、2cm×6cm×3cm=36cm3
右の長方形 X軸から図心までの距離は1cm
よって断面一次モーメントは、6cm×2cm×1cm=12cm3
2つを合わせると
36cm3+12cm3=48cm3
次に、図形全体(L型)で断面一次モーメントを考えます。求め方は同じです。
面積×軸から図心までの距離 です。
全体の面積は24cm2ですね
断面一次モーメントは先ほど求めた48cm3
わからないもの、つまり、求めたいものは、軸から図心までの距離です。
ということで式(面積×距離=断面一次モーメント)を立ててみますと
$$24cm^{3}×距離=48cm^{3}$$
となり、L型図形の図心は、X軸から2cmの位置ということになります。
断面二次モーメントを求める
2つの長方形に分けて求めます。先ほど求めた図形全体の図心軸に対して、それぞれの長方形の断面二次モーメントを求めます。
$$\frac {bh^{3}}{12}+bhyo^{2}$$
ここで、全体の図心軸と長方形の図心位置がずれていることに注意してください。
左右に分けた場合、全体の図心軸から各長方形の図心位置までの距離は、共に1cmとなります。つまり、yo はそれぞれ1です。
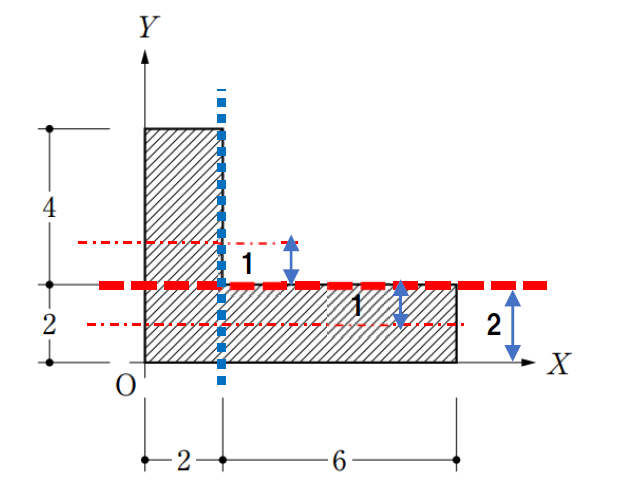
左の長方形
$$\frac {2×6^{3}}{12}+2×6×1^{2}=48cm^{4}$$
右の長方形
$$\frac {6×2^{3}}{12}+6×2×1^{2}=16cm^{4}$$
合計すると 48cm4+16cm4=64cm4 となります。
≪正解2≫
参考 図心の求め方
L型の図形を2つの長方形に分け、それぞれの図心を結びます。
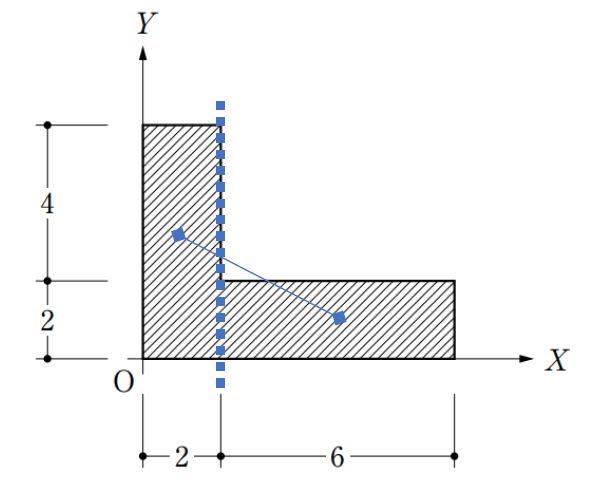
この結んだ線上に、L型図形の図心があります。
次に、長方形の分け方を左右から上下に変えてみます。
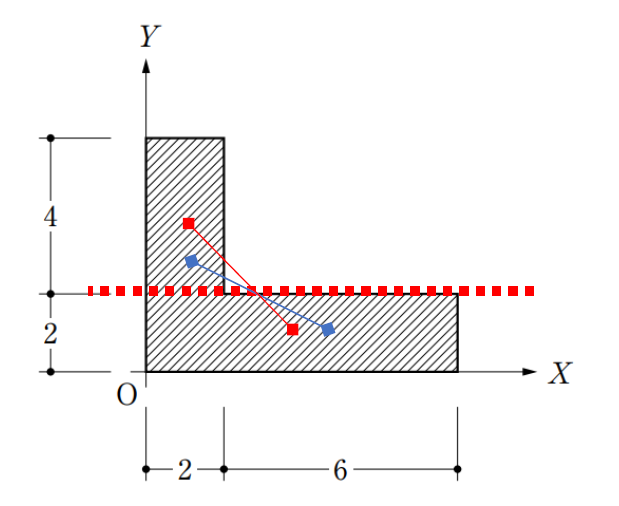
図心を赤い線で結ぶと、同じくこの線上にL型図形の図心があることになります。
つまり、2つの線の交わったところが、L型図形の図心ということになります。
2応力度・許容応力度
〔No. 2〕 図のような荷重 Pを受ける単純梁に、断面 300 mm×500 mmの部材を用いた場合、その部材に生じるせん断応力度が、許容せん断応力度 1 N/mm2を超えないような最大の荷重 Pとして、正しいものは、次のうちどれか。ただし、せん断力Qが作用する断面積 Aの長方形断面に生じる最大せん断応力度τmaxは、下式によって与えられるものとし、部材の自重は無視するものとする。
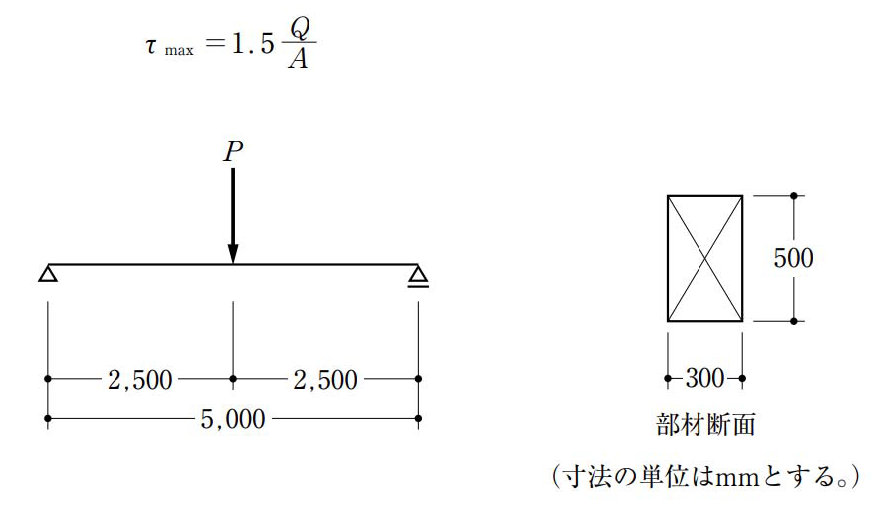
- 100 kN
- 150 kN
- 200 kN
- 250 kN
- 300 kN
ゆこ
この問題では、せん断応力度を求める公式が与えられていますが、この公式はできれば覚えるようにしてください。
解答と解説 詳細を見る
解き方のポイント
- 荷重をPとした時の反力を求め、せん断力(Q)を求める。
- せん断力の公式を用いて、Pの値を求める。
反力を求める
反力は荷重Pの半分になりますので、$$\frac {P}{2}$$です。

せん断力を求める
せん断力は、その点において、左側の荷重をそのまま合計します。
上向きの力を+としてください。
せん断力図を描くと下図のようになります。
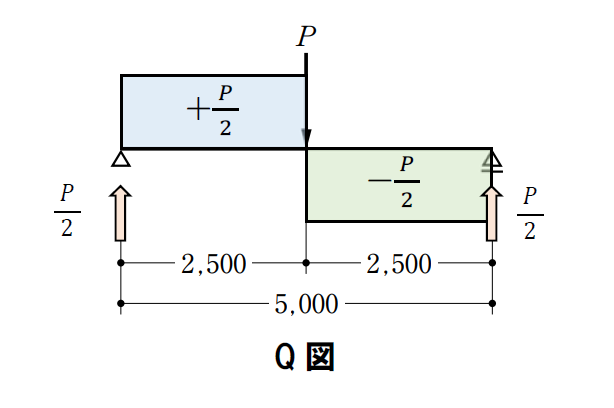
公式に代入する
$$τ max=1.5\frac{Q}{A}$$
τmaxに、設問で与えられている1を代入します。
Qは絶対値で考えればOKです。
Aの面積は、300×500ですね。
$$1=1.5×\frac{\displaystyle\frac{P}{2}}{300×500}$$
これを計算すると、Pは、200,000N
単位をkNにすると、200kNとなります。
≪正解3≫
3静定ばりの応力
〔No. 3〕 図のような荷重を受ける単純梁に生じる曲げモーメントの大きさの最大値として、正しいものは、次のうちどれか。
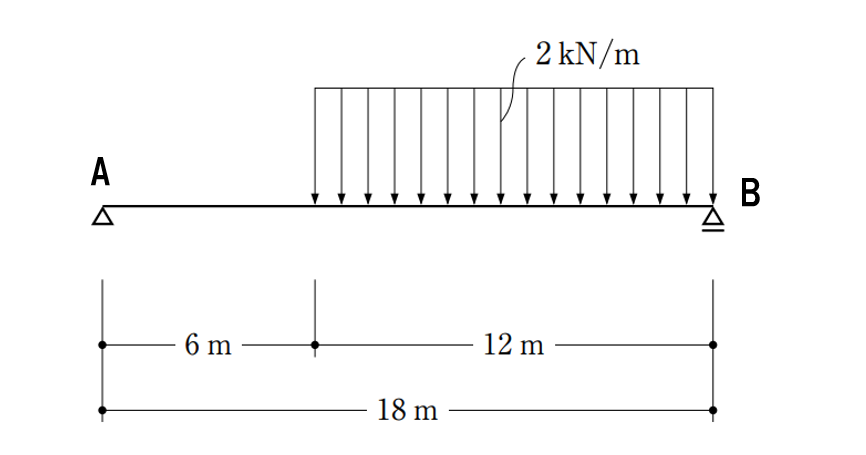
- 36 kN・m
- 48 kN・m
- 60 kN・m
- 64 kN・m
- 81 kN・m
ゆこ
この問題は一見既出かなと思ってしまいますが、曲げモーメントが最大になるところを見つけるのが少し難しいと言えます。この場合、等分布荷重がかかっている範囲の真ん中ではないんですよね。
解答と解説 詳細を見る
解き方のポイント
- 反力を求める。
- 曲げモーメントが最大になる位置を求める。
- その位置での曲げモーメントを求める。
反力を求める
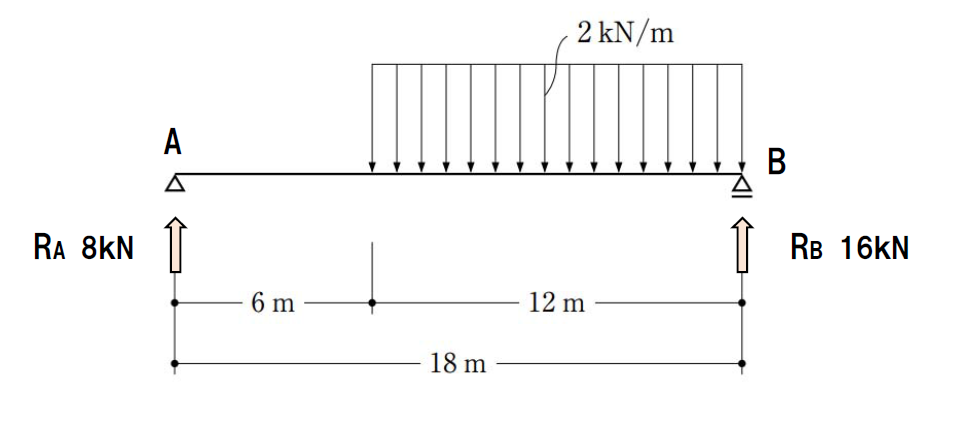
B点を基準につり合い方程式を立て、A点の反力(RA)を求めます。
RA×18-24×6=0 ⇒ RA=8kN
上からの等分布荷重は、2kN/m×12mで、24kN
鉛直方向の力はつり合いますので、RBは、16kNとなります。
曲げモーメントが最大になるところを探す
曲げモーメントが最大になるところは、せん断力が0になるところになります。
せん断力図で、プラスからマイナスになる位置を探します。
せん断力は、求めたい位置においてその点から左側の荷重を合計して求めます。
(上向きが+)
A点から8mの範囲は、反力の8kN。
等分布荷重がかかっている範囲は、B点に近づくにつれて、1mごとに2kNずつ減っていくことになり、B点に至ると-16kNになります。
せん断力図は下図のようになります。
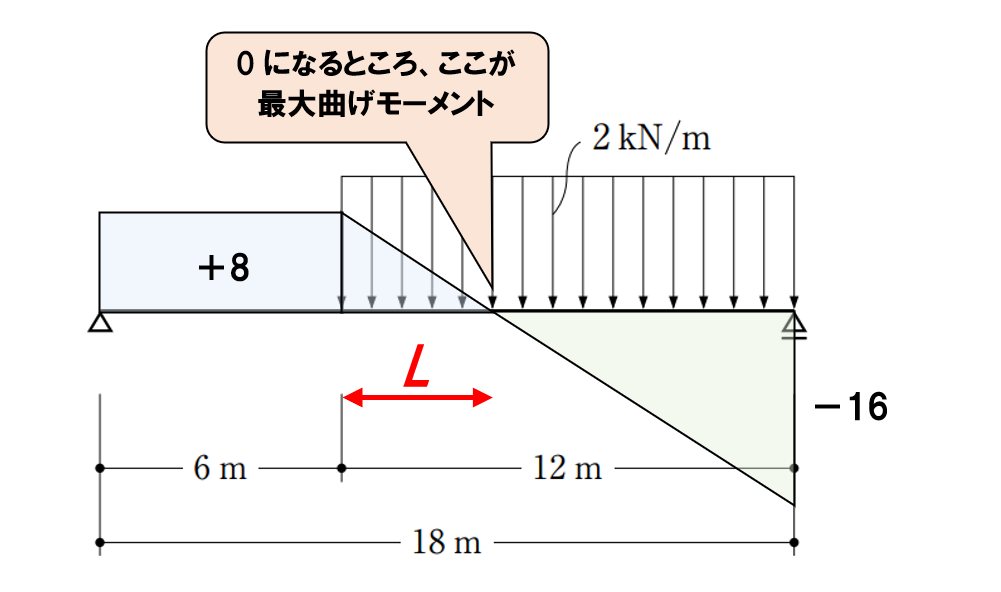
せん断力が0の位置は、次の式を満たすxの値を求めればOKです。
+8kN/m-2kN/m × L=0 ⇒ L=4
(8と16なので、12mを1:2に分けてもOKです。)
曲げモーメントを求める
A点から10m(6m+4m)の位置での曲げモーメントを求めます。
求めたい点から左側の荷重について、モーメントを合計してください。
8×10 -2×4×2 = 64kN・m
※上からかかっている等分布荷重を忘れないように注意してください。
≪正解4≫
4静定ラーメンの応力
〔No. 4〕 図のような外力を受ける静定ラーメンにおいて、支点Bに生じる鉛直反力RB、水平反力HBの値とE点に生じる曲げモーメントMEの絶対値との組合せとして、正しいものは、次のうちどれか。ただし、鉛直反力の方向は上向きを「+」、下向きを「-」とし、水平反力の方向は左向きを「+」、右向きを「-」とする。

|
|
| RB |
HB |
MEの絶対値 |
| -9kN |
-6kN |
0kN |
| +9kN |
-6kN |
54kN |
| +3kN |
+6kN |
36kN |
| +9kN |
+6kN |
12kN |
| +9kN |
+6kN |
18kN |
|
ゆこ
この問題はラーメン構造の問題です。構造力学としては比較的難しい問題に分類されますが、基本的な考え方が理解できていれば解くことができます。1つ1つのことは難しくないので、じっくり落ち着いて解くようにしてください。
解答と解説 詳細を見る
解き方のポイント
- この問題は、つり合い方程式を理解していれば解ける。
- 曲げモーメントは、左右どちらかのモーメント(力×距離)の合計。
- 間違えないように1つ1つ落ち着いて計算する。
水平反力HBを求める
Aはローラーなので、水平反力はありません。水平反力を負担するのはピンであるBです。
ラーメンに対して横向きにかかっている荷重は、1kN/mの水平力のみなので、HBは、
1kN/m×6m=6kN
(1kN/mの等分布荷重は右向きなので反力は左向き、したがって「+」です。)
鉛直反力RBを求める
A点を基準につり合い方程式(ΣM=0)を立てます。
(基準の点に対して時計回りの力を+とします)
1×6×3 + 2×6×3 -RB×6 = 0
⇒ RB=9kN
(上向きを想定して答えが+なので、想定通り上向きの力「+」となります。)
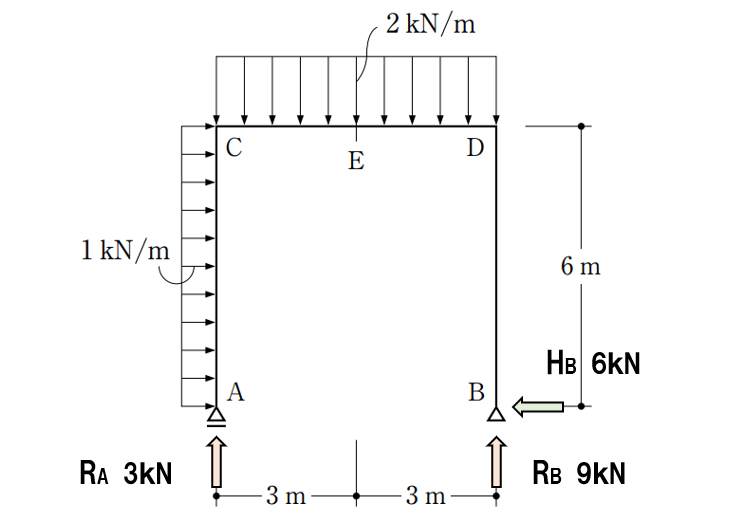
E点の曲げモーメントを求める
E点の右側の荷重に対して、モーメント(力×距離)を合計します。
右側の荷重は、2kN/mの等分布荷重(半分の3m)とHBの6kN、RBの9kN、この3つです。
2×3×1.5 +6×6 -9×3 = 18kN
ということで、答えは➎ということになりました。
最後のE点の曲げモーメントですが、左側でも同じ値になりますので確認しておきます。
(ただし、符号は変わります。)
ΣY=0より、RA +9(RB)-2×6(等分布荷重)= 0 ⇒ RA=3kN
E点の曲げモーメントを左側で計算すると
3(RA)×3 -1×6×3 -2×3×1.5 = -18kN
符号は違いますが、同じ18kNとなりました。最後のモーメントは絶対値を求めればいいので、計算するのは左右どちらでも構いません。できれば、両方計算してみて同じ数値になるか確認しておくとベターです。
≪正解5≫
5静定トラスの応力
〔No. 5〕 図のような荷重を受ける静定トラスにおいて、部材A、B、Cに生じる軸方向力の組合せとして、正しいものは、次のうちどれか。ただし、軸方向力は、引張力を「+」、圧縮力を「-」とする。なお、節点間距離は全て2mとする。
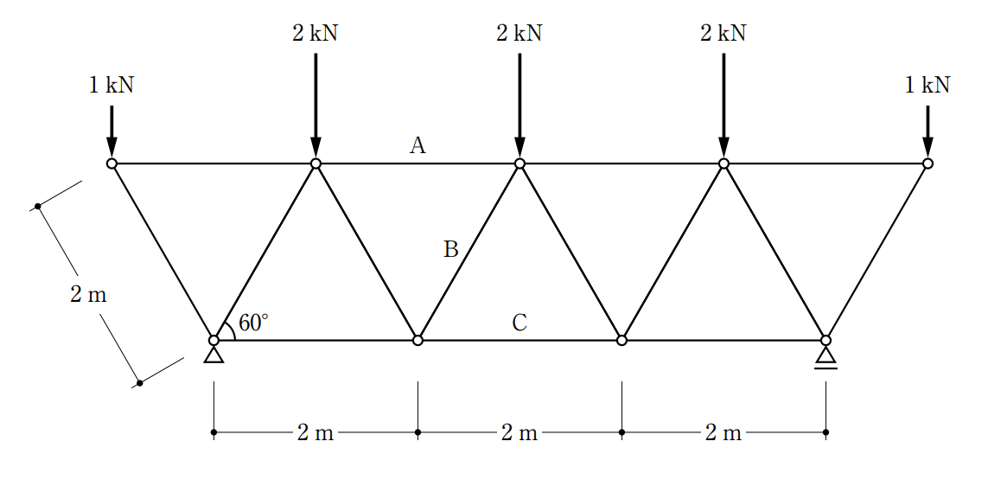
ゆこ
このトラスの問題も先ほどの問題と同じで、構造力学としては比較的難しい問題に分類されます。ただし、この問題も基本的な考え方が理解できていれば解くことができます。是非、挑戦してみてください。過去の比較的簡単なトラスの問題から解いてみるのもいいかもしれませんね。
解答と解説 詳細を見る
解き方のポイント
- つり合い方程式をきちんと理解しておくこと。
- この問題は、切断法で解く。
- 三角形の辺の比は覚えておこう。
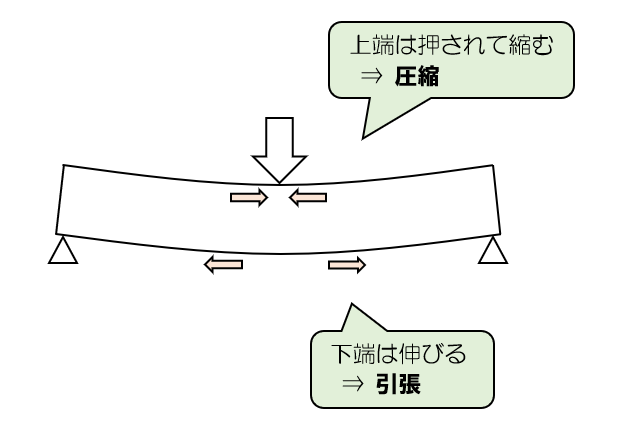
消しゴムなどやわらかいものをイメージしてみてください。上から荷重をかけると、下図のようにたわみます。
この時、上端は押されて縮んでいます。つまり圧縮「-」です。
下端は、引っ張られて伸びることになります。つまり引張「+」です。
このことより、部材Aは圧縮、部材Cは引張となりますので、トラスの解き方があまりわからなくても、正解は2か3であるという判断はできます。
反力を求める
まずは反力から求めていきましょう。
トラスの上部からかかっている5つの荷重を合計すると8kNです。トラスは左右対称になっていますので、左側のピンと右側のローラーが負担する反力は同じ、つまり、8kNを半分にすれば求まります。反力は、4kNです。
切断法で解く
トラスの解き方は主に節点法と切断法がありますが、この問題においては切断法で解くようにします。
切断法とは
求めたい部材を通る位置でトラスを切断します。この時、片側(左右どちらでもOK)に作用している荷重と、切断された部材の力がつり合います。この性質を利用して解く方法。
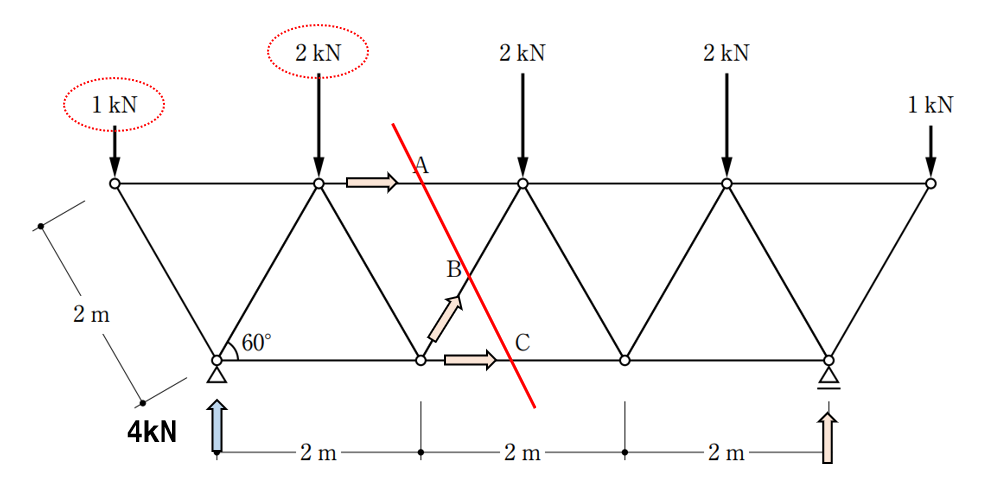
赤線位置で切断し、左側を見た場合、上からの荷重1kNと2kN、それから反力の4kN、切断された部材ABC、この6つの力がつり合います。つまり、ΣX=0、ΣY=0 ΣM=0 この3つの式が成り立ちます。
部材ABCの力の向きは赤線側としていますが、これは反対を想定しても構いません。計算を行ない、結果が「+」となる場合は想定した向き、結果が「-」となる場合は想定した向きと反対の向きに力が作用していることになります。
では、部材Aから求めていきましょう。
部材Aを求める場合は、BとCの交点を基準にモーメントのつり合い (ΣM=0) を考えます。そうすると、部材BとCは、それぞれの距離が0になりますので、BとCのモーメントは0になり、計算において考慮する必要がなくなります。
-1kN×3m -2kN×1m +4kN×2m +A×√3m = 0 ⇒ A=-√3kN
答えがマイナスとなりましたので、想定していた右向きとは反対で左向きとなります。節点に向かう向きなので、部材Aは圧縮(-)となります。
同じように、部材Cを求める場合は、AとBの交点を基準にモーメントのつり合い (ΣM=0) を考えます。
-1kN×4m -2kN×2m +4kN×3m -C×√3m = 0 ⇒ C=kN
答えがプラスとなりましたので、想定していた通り右向き。節点から離れる向きなので引張(+)です。
最後部材Bですが、部材Bは、鉛直方向のつり合い (ΣY=0) を考えます。
斜めになっていますので、縦の成分と横の成分に分けてください。
-1kN -2kN +4kN +Bの縦の成分 = 0 ⇒ Bの縦の成分=-1kN
答えがマイナスなので、想定とは反対の下向き。節点に向かう向きなので圧縮(-)です。
縦成分が1なので、三角形の比より、部材Bそのものの力は、2√3/3kN (圧縮)となります。
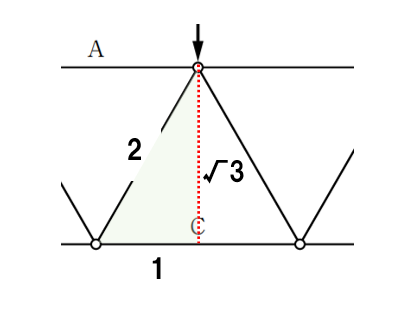
√3のところが1となりますので、斜め部分の部材Bは
1kN:B = √3:2
この関係より求めることができます。
≪正解2≫
6座屈
〔No. 6〕 図のような長さl (m)の柱(材端条件は、両端ピン、水平移動拘束とする。)に圧縮力Pが作用したとき、次のlとIとの組合せのうち、弾性座屈荷重が最も大きくなるものはどれか。ただし、Iは断面二次モーメントの最小値とし、それぞれの柱は同一の材質で、断面は一様とする。
|
|
| l(m) |
I(m4) |
| 3.0 |
3×10-5 |
| 3.5 |
4×10-5 |
| 4.0 |
5×10-5 |
| 4.5 |
7×10-5 |
| 5.0 |
8×10-5 |
|
ゆこ
この問題は過去に何度か出題されている問題です。確実にできるようになっておきたいと言えます。
解答と解説 詳細を見る
解き方のポイント
- 座屈荷重を求める公式は確実に覚えておくこと。
- 計算はなるべく簡単に。
弾性座屈荷重(部材が座屈する時の荷重)を表わす式(オイラーの公式)は、
$$\frac {π^2 EI}{lk^2}$$
です。
設問より、材質が同じなので、πとEは無視し、$$\frac {I}{lk^2}$$
この部分だけを比較します。
この時、lk は、材の長さではなく座屈長さであることに注意してください。材端条件により、座屈長さは違ってきます。
ただ、この問題における材端条件は両端ピン、水平拘束なので、座屈長さは部材の長さと等しくなります。lk=l です。
1から5までを式に代入してみると
| ➊ |
$$\frac {I}{lk^2} $$ |
$$=\frac {3×10^{-5}}{3^{2}}$$ |
$$=\frac {3×10^{-5}}{9}$$ |
| ➋ |
$$\frac {I}{lk^2} $$ |
$$=\frac {4×10^{-5}}{3.5^{2}}$$ |
$$=\frac {4×10^{-5}}{12.25}$$ |
| ➌ |
$$\frac {I}{lk^2} $$ |
$$=\frac {5×10^{-5}}{4^{2}}$$ |
$$=\frac {5×10^{-5}}{16}$$ |
| ➍ |
$$\frac {I}{lk^2} $$ |
$$=\frac {7×10^{-5}}{4.5^{2}}$$ |
$$=\frac {7×10^{-5}}{20.25}$$ |
| ➎ |
$$\frac {I}{lk^2} $$ |
$$=\frac {8×10^{-5}}{5^{2}}$$ |
$$=\frac {8×10^{-5}}{25}$$ |
この計算をして一番大きいものを見つけることになりますが、少し面倒ですよね。
まず、10-5をなくしてください。
次に、分母と分子を反対にして、反対に答えが一番小さくなるものを見つけるようにします。
そうすると、計算が楽になります。
代入してみると
| ➊ |
9÷3 |
=3 |
| ➋ |
12.25÷4 |
≒3.06 |
| ➌ |
16÷5 |
=3.2 |
| ➍ |
20.25÷7 |
≒2.89 |
| ➎ |
25÷8 |
≒3.12 |
一番値が小さくなった4が、一番座屈荷重が大きいということになります。
≪正解4≫
かんな先生
以上、二級の構造力学の問題を見ていただきましたが、6問のうち4つの問題で力のつり合いの考え方が出てきています。力のつり合いは構造力学においてとても重要なので、しっかりと理解しておくようにしたいですね。
それから、この6つの出題(1断面の性質、2応力度・許容応力度、3静定ばりの応力、4静定ラーメンの応力、5静定トラスの応力、6座屈)ですが、この項目と出題順序はこの10年変わっていません。今後も出題されると思いますので、1つでも多く攻略しておきたいですね。










































